Dim x As New Matrix(New Double() {1, 2, 3, 4}, New Integer() {2, 2})
Dim e0 As Double = x(0)
' 1
Dim e3 As Double = x(3)
' 4
This topic demonstrates the operations you can perform with Matrices. It covers Matrix instances only, but the information in it applies to all matrix types – Matrix, BooleanMatrix, and ComplexMatrix.
The operations supported by matrices fall into the following basic categories:
Each of them is explained in an individual section.
Indexing retrieves the element at a particular position in the matrix.
In the Infragistics Math Library, matrices can be indexed as arrays:
In Visual Basic:
Dim x As New Matrix(New Double() {1, 2, 3, 4}, New Integer() {2, 2})
Dim e0 As Double = x(0)
' 1
Dim e3 As Double = x(3)
' 4
In C#:
Matrix x = new Matrix(new double[] { 1, 2, 3, 4 }, new int[] { 2, 2 });
double e0 = x[0]; // 1
double e3 = x[3]; // 4
Matrices can be indexed one-dimensionally with a vector of indices. This results in a one-dimensional row matrix containing the elements from the initial matrix which were at the positions defined by the vector:
In Visual Basic:
'x
' 1 4 7
' 2 5 8
' 3 6 9
Dim dimensions As Integer() = New Integer() {3, 3}
Dim elements As Double() = New Double() {1, 2, 3, 4, 5, 6, 7, 8, 9}
Dim x As New Matrix(elements, dimensions)
Dim ind As Vector = New Double() {0, 3, 8}
Dim y As Matrix = x(ind)
' x[0]=1, x[3]=4, x[8]=9
' y={ 1, 4, 9 }
In C#:
//x
// 1 4 7
// 2 5 8
// 3 6 9
int[] dimensions = new int[] { 3, 3 };
double[] elements = new double[] { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
Matrix x = new Matrix(elements, dimensions);
Vector ind = new double[] { 0, 3, 8 };
Matrix y = x[ind];
// x[0]=1, x[3]=4, x[8]=9
// y={ 1, 4, 9 }
In multi-dimensional indexing, elements are retrieved as per their coordinates in the matrix (In a two-dimensional matrix, the coordinates would be the row number and the column number):
In Visual Basic:
Dim x As New Matrix(New Double() {1, 2, 3, 4}, New Integer() {2, 2})
Dim c0 As Double = x(0, 0)
' 1
Dim c3 As Double = x(1, 1)
' 4
In C#:
Matrix x = new Matrix(new double[] { 1, 2, 3, 4 }, new int[] { 2, 2 });
double c0 = x[0,0]; // 1
double c3 = x[1,1]; // 4
In multi-dimensional indexing with Vectors, elements are retrieved as per their coordinates and the coordinates are created by two vectors.
For example, let’s have two vectors:
ind1 = { 0, 1, 1 }
ind2 = { 2, 1 }
Let these vectors form a new matrix containing pairs of indices (Figure 1):
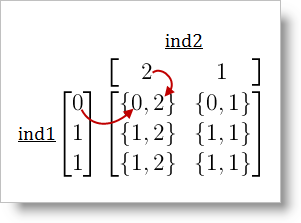
Figure 1: Matrix with pairs of indices.
After multi-dimensional indexing of the target matrix with vectors, a new matrix will be formed – it will have the dimensions of the matrix from Figure 1, and its elements are going to be the ones from the target matrix with positions {0, 2}, {1, 2}, … .
The code below creates a matrix and two vectors and uses the vectors to retrieve elements from the matrix in a multi-dimensional manner:
In Visual Basic:
'x
' 1 4 7
' 2 5 8
' 3 6 9
Dim dimensions As Integer() = New Integer() {3, 3}
Dim elements As Double() = New Double() {1, 2, 3, 4, 5, 6, 7, 8, 9}
Dim x As New Matrix(elements, dimensions)
Dim ind1 As Vector = New Double() {0, 1, 1}
Dim ind2 As Vector = New Double() {2, 1}
'The two vectors will form an indexing matrix:
' 0,2 0,1
' 1,2 1,1
' 1,2 1,1
Dim y As Matrix = x(ind1, ind2)
'Initial Matrix with Result
'matrix indices
' 1 4 7 0,2 0,1 7 4
' 2 5 8 1,2 1,1 8 5
' 3 6 9 1,2 1,1 8 5
In C#:
//x
// 1 4 7
// 2 5 8
// 3 6 9
int[] dimensions = new int[] { 3, 3 };
double[] elements = new double[] { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
Matrix x = new Matrix(elements, dimensions);
Vector ind1 = new double[] { 0, 1, 1 };
Vector ind2 = new double[] { 2, 1 };
//The two vectors will form an indexing matrix:
// 0,2 0,1
// 1,2 1,1
// 1,2 1,1
Matrix y = x[ind1, ind2];
//Initial Matrix with Result
//matrix indices
// 1 4 7 0,2 0,1 7 4
// 2 5 8 1,2 1,1 8 5
// 3 6 9 1,2 1,1 8 5
Arithmetical operations are supported by Matrix and ComplexMatrix types only.
Infragistics Math Library’s matrices support the following arithmetical operations:
addition (+)
subtraction (-)
multiplication (* )
division (/)
division with remainder (%)
The arithmetical operations are performed on the counterpart elements of the matrices.
The Matrix class also supports arithmetical operations between a matrix and a complex number.
Matrices must have the same dimensions.
The code below adds a double to a matrix:
In Visual Basic:
'x
' 1 3
' 2 4
Dim x As New Matrix(New Double(,) {{1, 2}, {3, 4}})
'y
' (1+2) (3+2)
' (2+2) (4+2)
Dim y As Matrix = x + 2
In C#:
//x
// 1 3
// 2 4
Matrix x = new Matrix(new double[,] { { 1, 2 }, { 3, 4 } });
//y
// (1+2) (3+2)
// (2+2) (4+2)
Matrix y = x + 2;
Multiplication of matrices in the Infragistics Math Library consists of multiplying the counterpart elements in matrices with the same dimensions using the * operator. This operation is different from true matrix multiplication as defined in mathematics.
Note:
If you want true matrix multiplication, use the Compute.MatrixProduct method instead of the multiplication shown here.
The example below multiplies two matrices using the * operator.
In Visual Basic:
'x
' 1 3
' 2 4
Dim x As New Matrix(New Double(,) {{1, 2}, {3, 4}})
'y
' 1 2
' 1 2
Dim y As New Matrix(New Double(,) {{1, 1}, {2, 2}})
'z
' (1*1) (3* 2)
' (2*1) (4* 2)
Dim z As Matrix = x * y
In C#:
//x
// 1 3
// 2 4
Matrix x = new Matrix(new double[,] { { 1, 2 }, { 3, 4 } });
//y
// 1 2
// 1 2
Matrix y = new Matrix(new double[,] { { 1, 1 }, { 2, 2 } });
//z
// (1*1) (3* 2)
// (2*1) (4* 2)
Matrix z = x * y;
Logical operations are supported by BooleanMatrix only. They can be performed:
between matrices
between a Boolean matrix and Boolean variable
When performed between matrices:
logical AND and OR are executed on the counterpart elements
logical NOT is executed on each element
When performed between a Boolean matrix and Boolean variable, the operation is performed on each element of the matrix and the variable.
Logical operations return a new Boolean matrix.
AND (&)
OR (|)
NOT (!)
Matrices must have the same dimensions.
The following example creates two BooleanMatrix instances and demonstrates how to use them in the logical operations NOT, AND, and OR:
In Visual Basic:
'x
' true false
' true false
Dim x As New BooleanMatrix(New Boolean(,) {{True, True}, {False, False}})
'y
' true true
' false false
Dim y As New BooleanMatrix(New Boolean(,) {{True, False}, {True, False}})
'NOT
' false true
' false true
Dim NOT_x As BooleanMatrix = Not x
'AND
' true false
' false false
Dim x_AND_y As BooleanMatrix = x And y
'OR
' true true
' true false
Dim x_OR_y As BooleanMatrix = x Or y
In C#:
//x
// true false
// true false
BooleanMatrix x = new BooleanMatrix(new bool[,] { { true, true }, { false, false } });
//y
// true true
// false false
BooleanMatrix y = new BooleanMatrix(new bool[,] { { true, false }, { true, false } });
//NOT
// false true
// false true
BooleanMatrix NOT_x = !x;
//AND
// true false
// false false
BooleanMatrix x_AND_y = x & y;
//OR
// true true
// true false
BooleanMatrix x_OR_y = x | y;
Infragistics Math Library’s matrices support the following operations for comparison:
equal to (==)
not equal to (!=)
greater than (>)
less than (<)
greater than or equal to (>=)
less than or equal to (<=)
These operations are performed on counterpart elements of the matrices.
The == and != operators compare the elements and the dimensions of the matrices and return a Boolean value.
The <, <=, >, and >= operators compare the corresponding values in the matrices. These operators return a BooleanMatrix instance and are defined only for Matrix and ComplexMatrix. Each element of the returned Boolean matrix will be the result of the comparison of the corresponding elements from the initial matrices.
Matrix and ComplexMatrix can be compared to each other and to double and Complex. BooleanMatrix can be compared also to a Boolean value.
Matrices must have the same dimensions.