Exploraciones visuales del tamaño de la muestra

Sacar conclusiones basadas en muestras pequeñas es obviamente problemático. Al mismo tiempo, también me pregunto si el aumento de la prominencia del "Big Data" puede llevar a las organizaciones a recopilar ciegamente la mayor cantidad de datos posible en lugar de pensar lógicamente sobre la cantidad de datos que realmente se necesitan para realizar las tareas de análisis que se requieran.

Prefiero tener un poco más de datos de los necesarios que no sean suficientes, pero eso no significa que debamos recopilar todo solo porque podemos. Podemos usar estadísticas para guiarnos en cuanto a la cantidad de datos que realmente necesitamos, pero recientemente me puse a pensar en cómo podemos mostrar visualmente qué efecto tiene el aumento del tamaño de la muestra.

Para simplificar las cosas, me limitaré a observar el efecto de aumentar el tamaño de la muestra con variables aleatorias a partir de una instancia específica (pero bastante arbitraria) de la distribución normal. Dejaré la indicación de los parámetros, la media verdadera y la desviación estándar verdadera, para más adelante.

El gif animado a continuación muestra histogramas de densidad de probabilidad realizados a partir del muestreo de la distribución normal antes mencionada. De fotograma a fotograma, el tamaño de la muestra aumenta por diez, y los datos utilizados para dibujar cada histograma son un superconjunto de los datos del fotograma anterior. La curva roja es la distribución normal con la misma media y desviación estándar que los datos de la muestra.

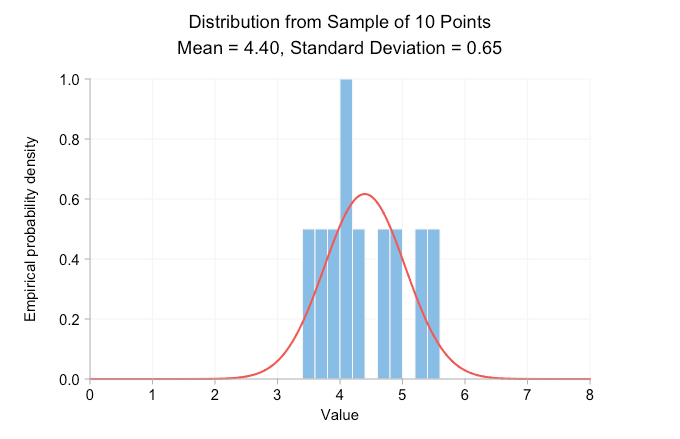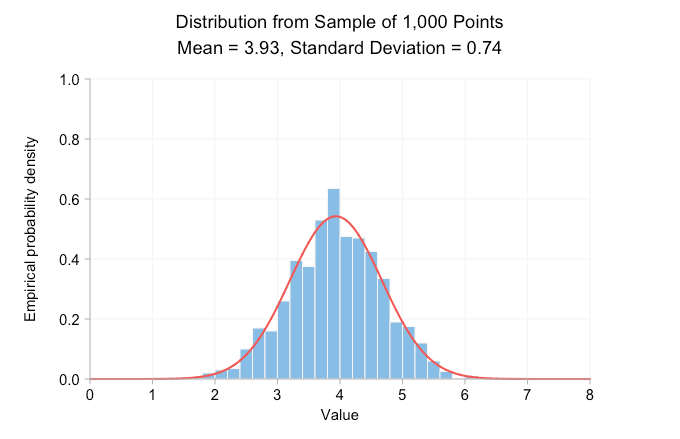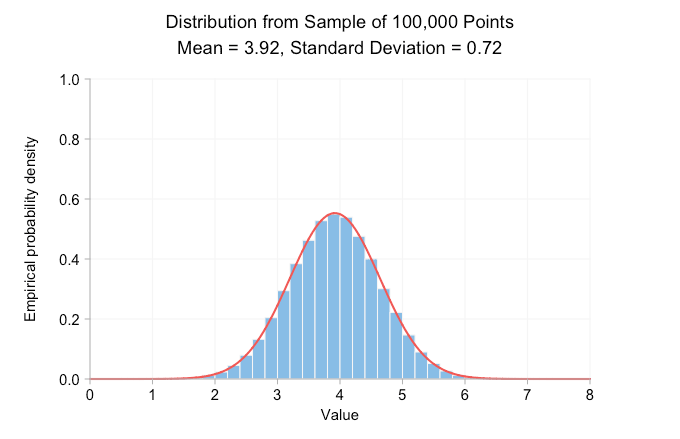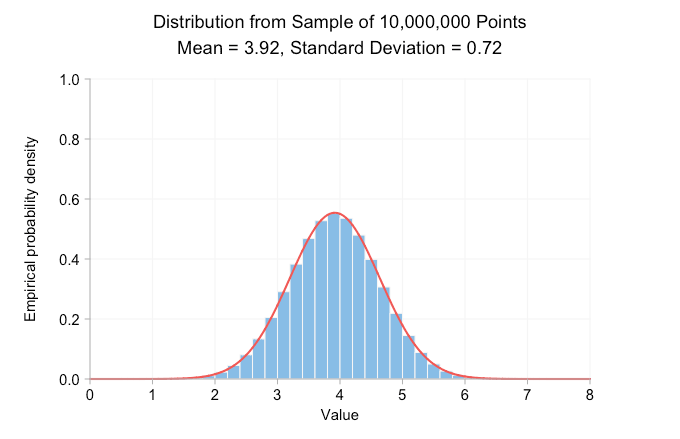
Claramente, con un tamaño de muestra de solo diez, la distribución empírica no se parece en nada a la distribución normal con la misma media y desviación estándar. Todo lo que realmente podemos decir de esto es que la verdadera media es probablemente en algún lugar cercano a 4 o 5. Pero si aumentamos la muestra a 100 puntos, ya podemos ver una curva de campana aproximada. Para cuando llegamos a los 100.000 puntos, tenemos una muy buena coincidencia visual entre el histograma y la curva. Agregar más puntos no cambia el aspecto de la distribución ni la media y la desviación estándar impresas.

El histograma animado es bueno para dar una visión general de cómo cambian las cosas a medida que añadimos más puntos, pero con un solo fotograma por cada factor de 10 no vemos una imagen muy detallada. Si no se imprimen más dígitos en los parámetros del título en la parte superior, no está claro con qué precisión conocemos la media y la desviación estándar para cualquier tamaño de muestra en particular. Para tener una mejor idea de esto, podemos elegir un parámetro y trazarlo en función del tamaño de la muestra, desde 2 puntos (cuando ambos parámetros de la muestra son finitos) hasta diez millones. Primero veremos la media.

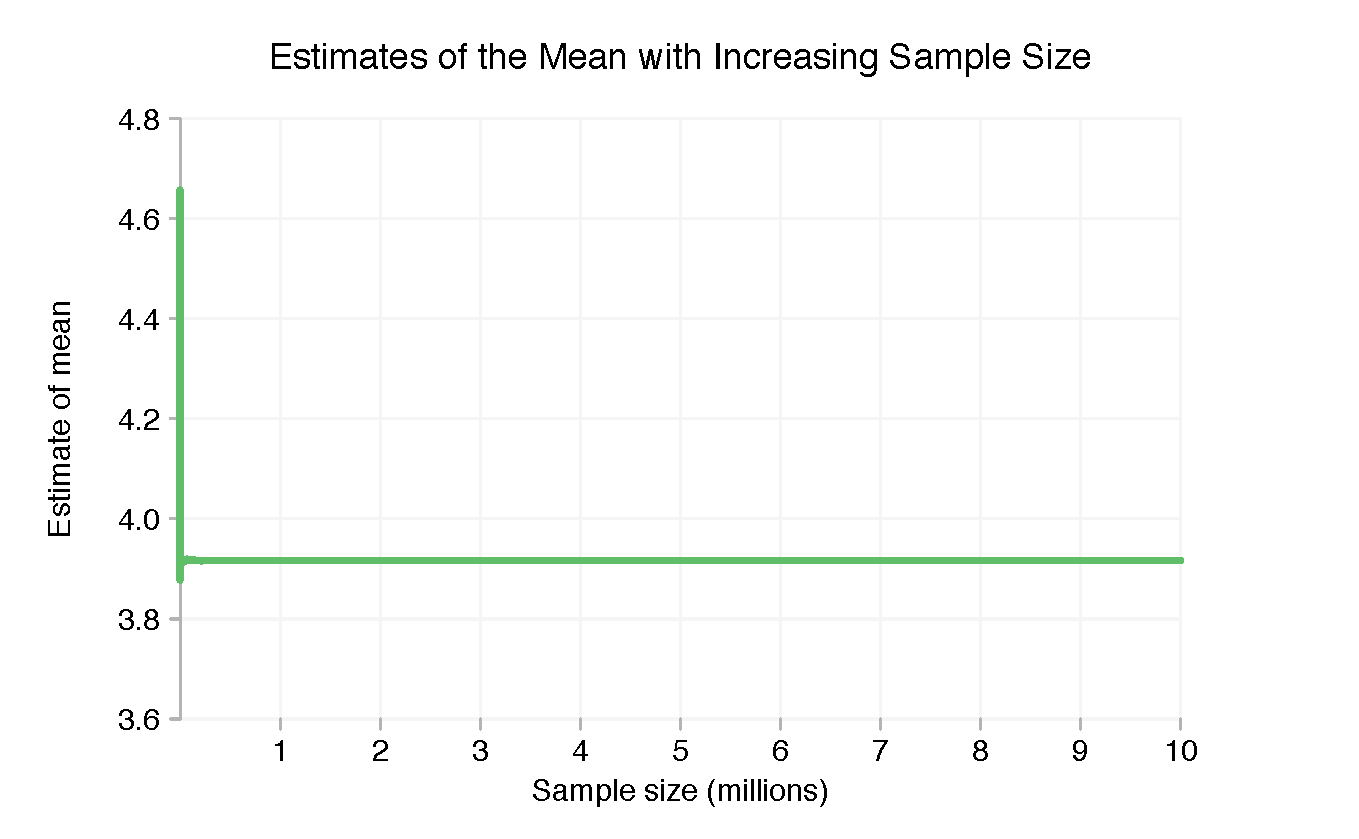
Debido a que las cosas cambian mucho más rápido cuando solo hay una pequeña cantidad de datos, el gráfico anterior es bastante inútil. Tomar el logaritmo (base 10) del número de puntos en la muestra hace las cosas mucho más claras.

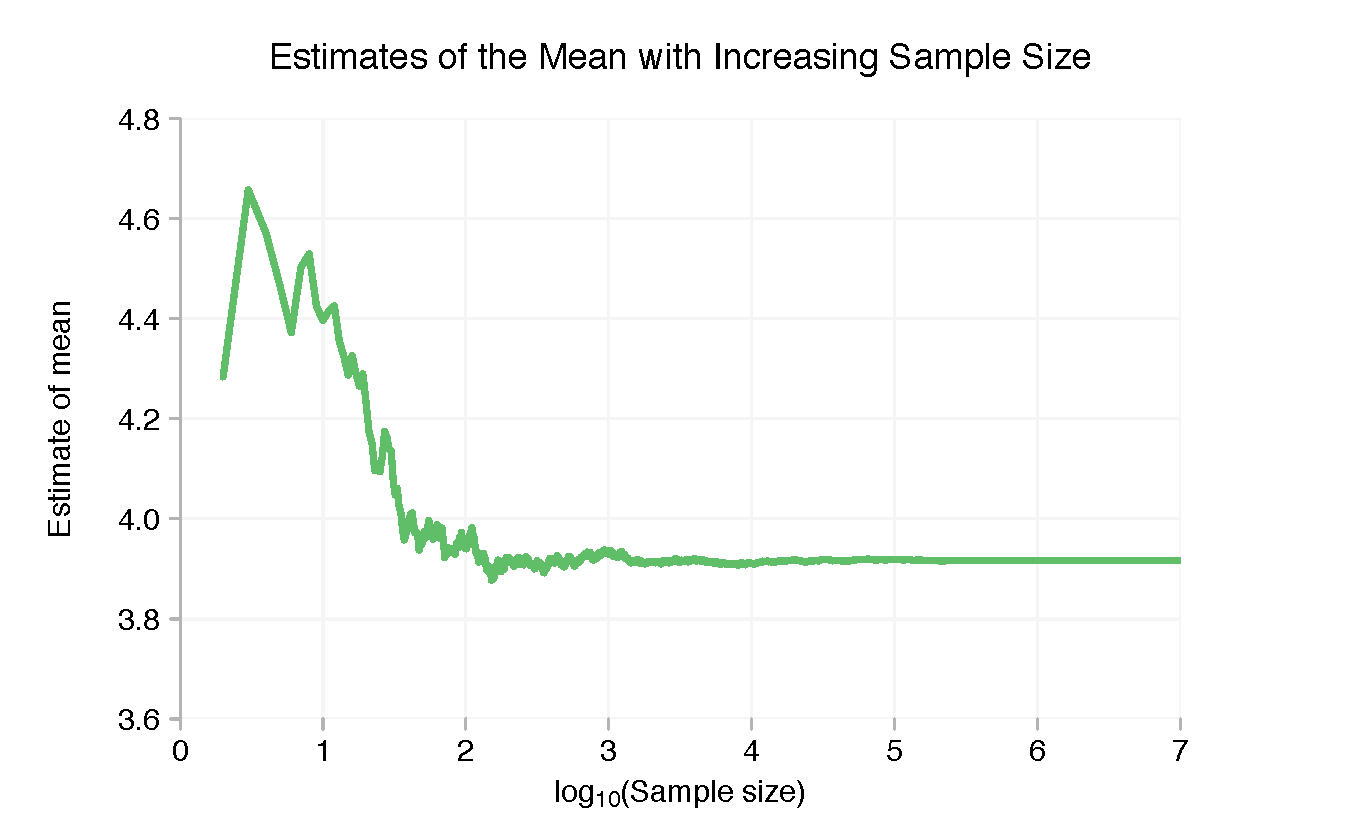
Con pocos puntos, la media muestral está muy por encima de 4. Pero esto cae rápidamente y se estabiliza una vez que estamos en los dos dígitos. Más allá de unos pocos miles de puntos, hay poca variación discernible en la media de la muestra, pero podemos acercarnos en el lado derecho y ver el "bamboleo" más fino.

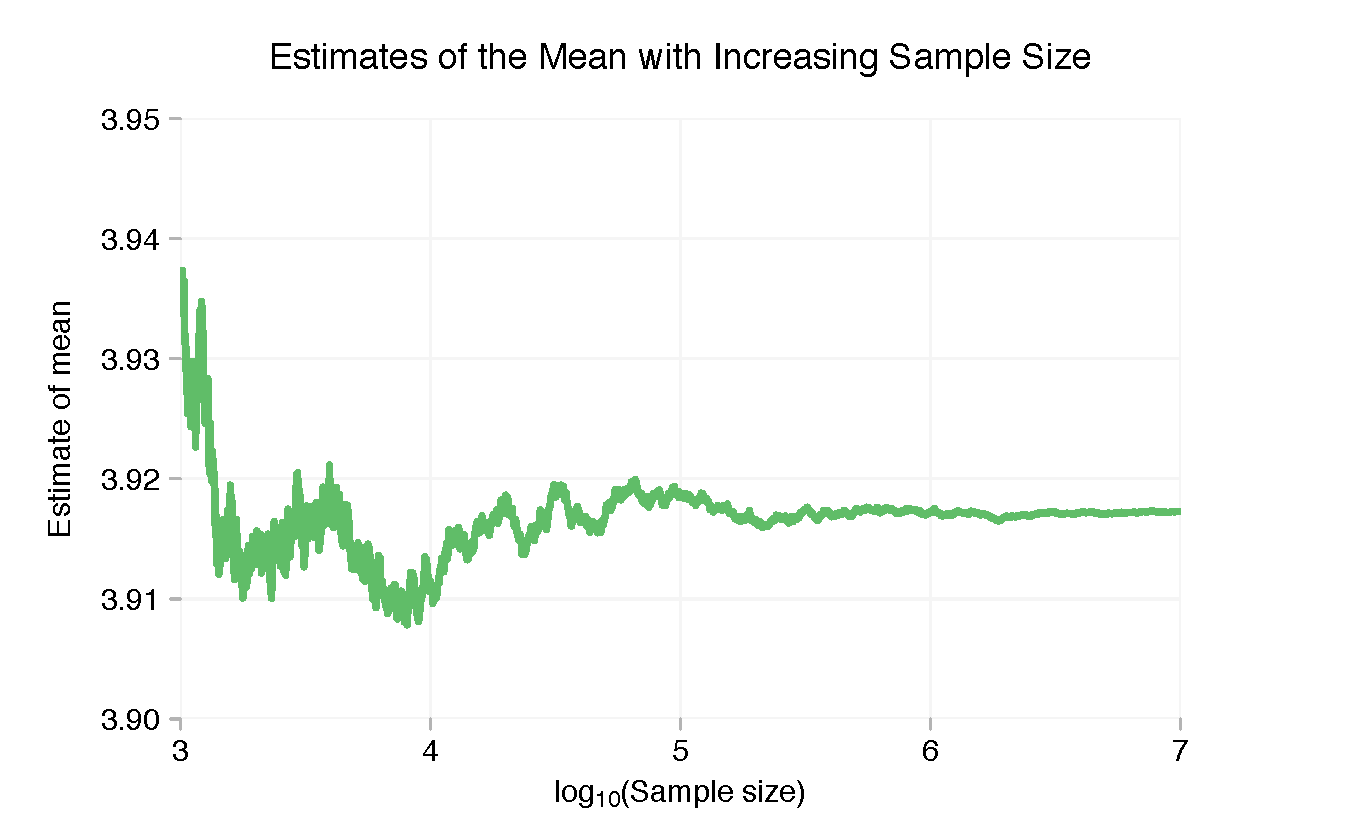
Así es como cambia la desviación estándar a medida que cambiamos el tamaño de la muestra (nota: ¡esta es la desviación estándar de la muestra, no el error estándar de la media!):

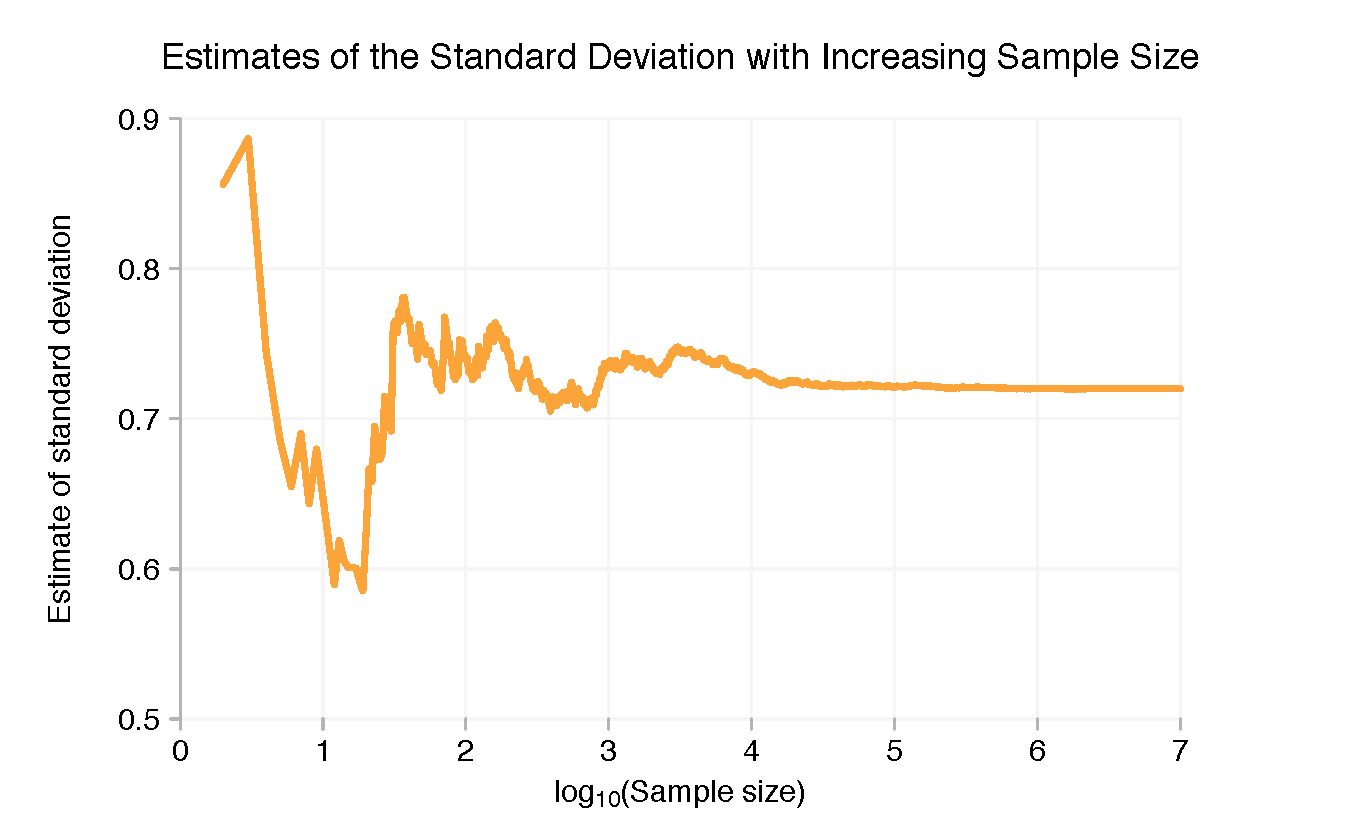
La media real utilizada para generar la muestra fue de 3,9172 y la desviación estándar de 0,7200. Podemos ver en los gráficos que nos hemos acercado bastante a estos números con diez millones de puntos de datos sin hacer ningún análisis estadístico riguroso. Pero tampoco estábamos tan lejos, a diez mil puntos de datos. Más datos significan más precisión, pero si todo lo que necesitabas saber era si la media era mayor o menor que 4, ~1.000 puntos habrían sido suficientes.

Para reforzar el punto, echemos un vistazo solo a los primeros 100.000 puntos de datos y dividámoslos en diez muestras de 10.000. Con cada submuestra podemos utilizar la misma técnica gráfica que antes. Las líneas de colores en los gráficos a continuación muestran los resultados de los primeros 10.000 puntos de datos, las líneas grises las otras submuestras.

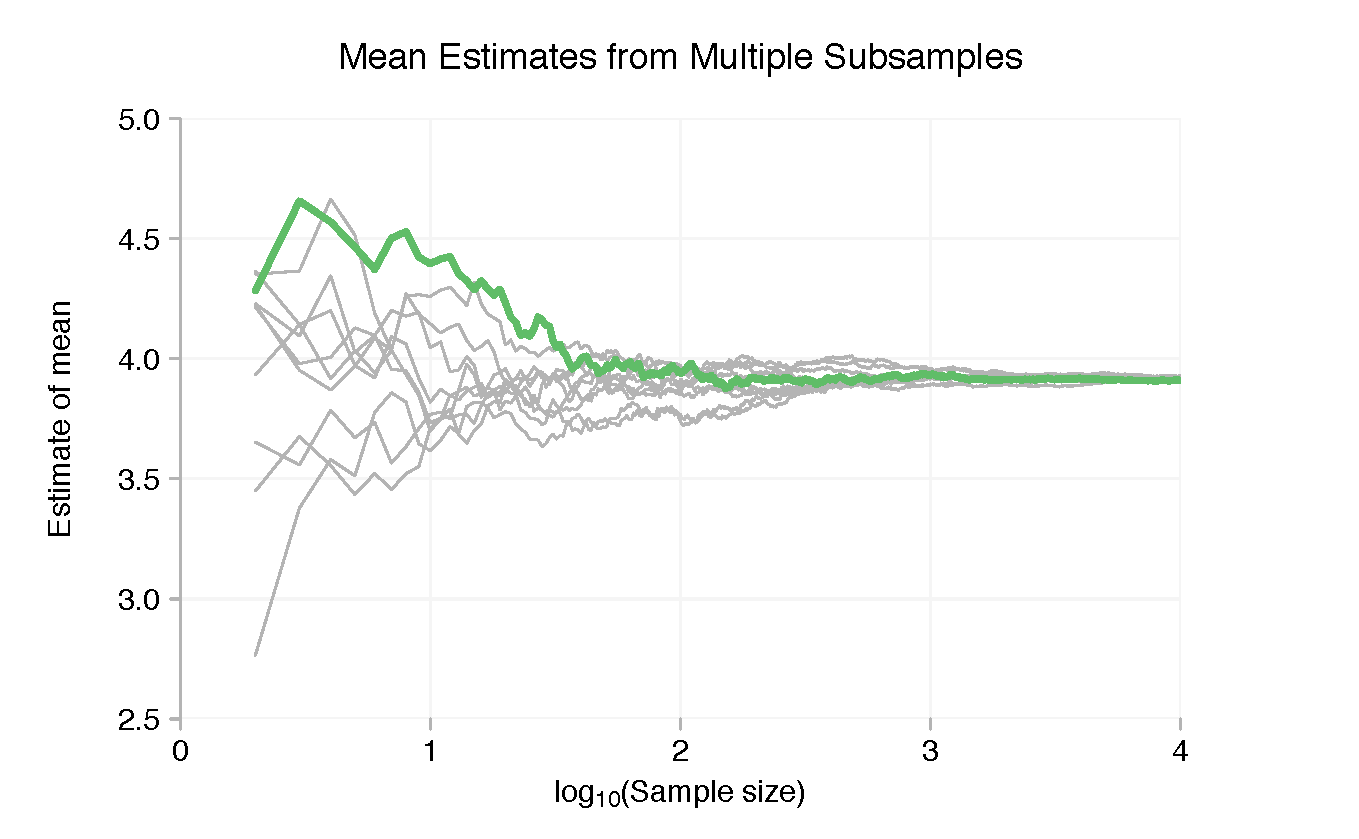
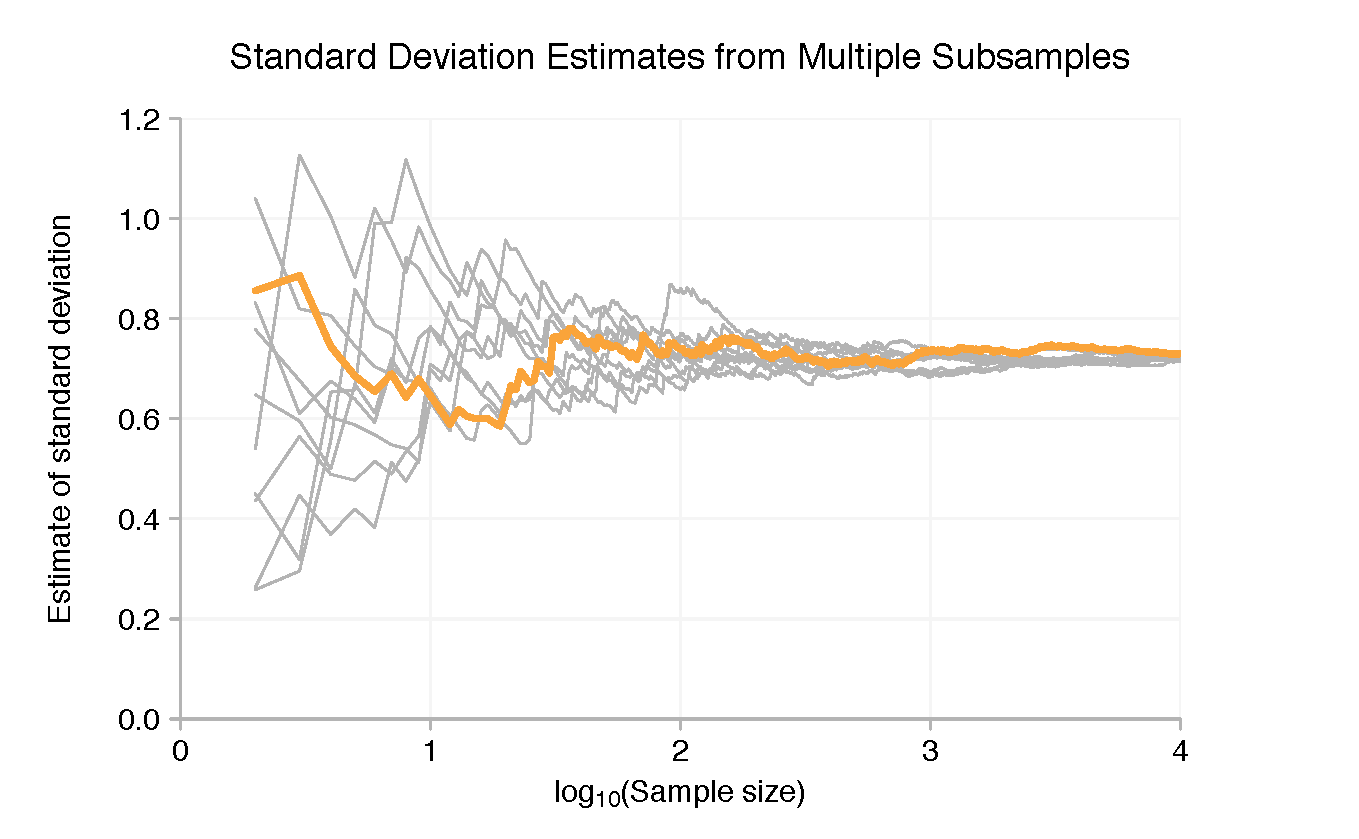
Para ser claros, el propósito de los gráficos no es realmente ver las pistas individuales hechas por una submuestra. Es para mostrar que las medias y desviaciones estándar de las submuestras se distribuyen ampliamente cuando cada una tiene solo unos pocos puntos de datos pero, al menos en una escala logarítmica, convergen rápidamente a medida que agregamos más puntos.

Por supuesto, todos los conjuntos de datos son diferentes y muchos no se obtienen a través de un simple muestreo aleatorio. Tampoco puede asumir que su conjunto de datos del mundo real se comportará tan bien como una gran colección de variables aleatorias generadas por computadora a partir de una sola instancia de la distribución normal. Además, las ideas de gráficos anteriores no pretenden ser sustitutos directos del riguroso trabajo estadístico. Pero en ciertos casos pueden complementarlo, por ejemplo, proporcionando una verificación de cordura de una evaluación estadística o como una alternativa visual para una audiencia con menos experiencia técnica.

¿Busca una herramienta de creación de prototipos completa y rápida, que le permita ver exactamente cómo se verá y funcionará su compilación incluso antes de escribir un solo código de línea? No busques más.¡Descargue nuestra versión de prueba gratuita de Indigo Studioahora y vea lo que puede hacer por usted!