Too Big Data: Cómo hacer frente al exceso de trazado

Con todo el revuelo en torno al Big Data en los últimos años, es fácil suponer que tener más datos siempre es una ventaja. Pero a medida que añadimos más y más puntos de datos a un diagrama de dispersión, podemos empezar a perder estos patrones y clústeres. Este problema, resultado de un sobretrazado, se muestra en la siguiente animación.

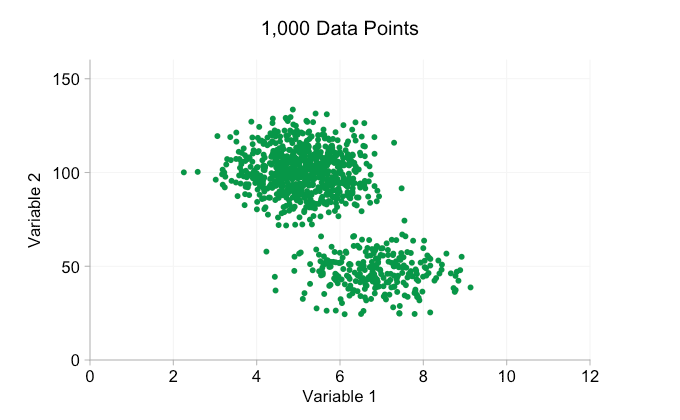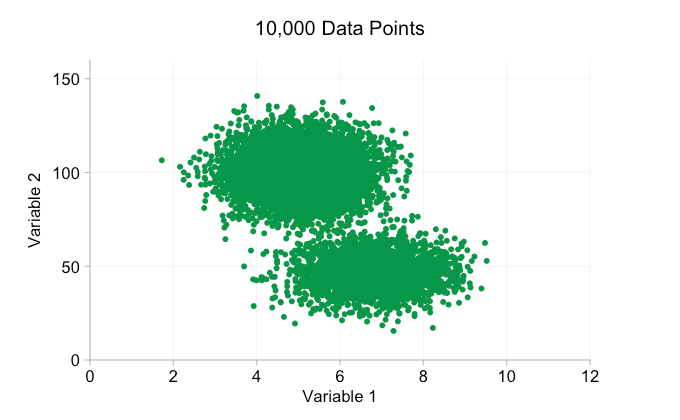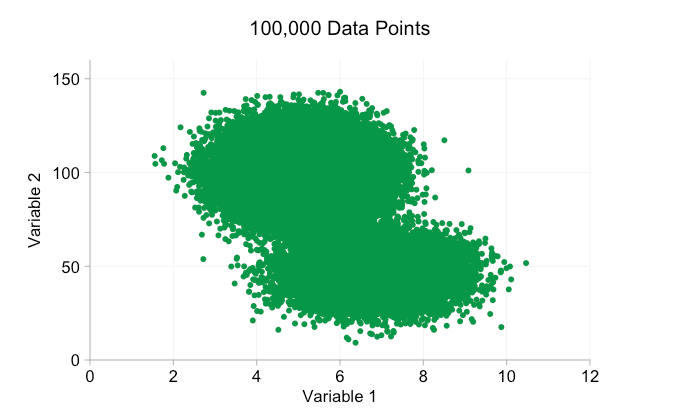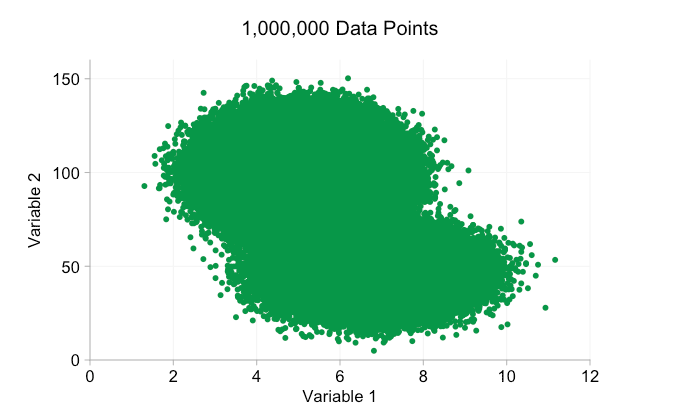
Los datos de la animación anterior se generan aleatoriamente a partir de un par de distribuciones bivariadas simples. La distinción entre las dos distribuciones se vuelve cada vez menos clara a medida que agregamos más y más datos. Entonces, ¿qué podemos hacer con el sobreploting?

Una opción sencilla es hacer que los puntos de datos sean más pequeños. (Tenga en cuenta que esta es una mala "solución" si muchos puntos de datos comparten exactamente los mismos valores). También podemos hacerlos semitransparentes. Y podemos combinar estas dos opciones:

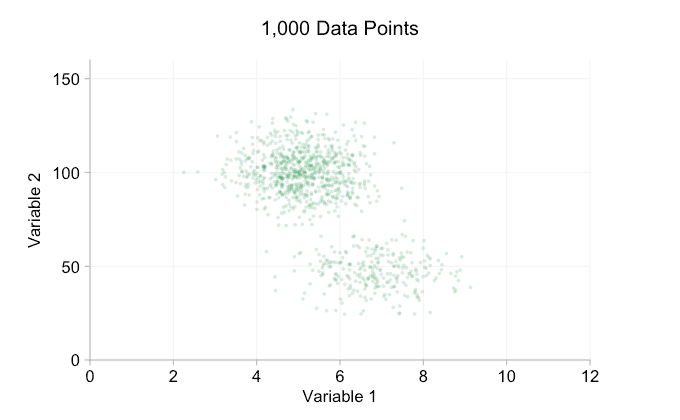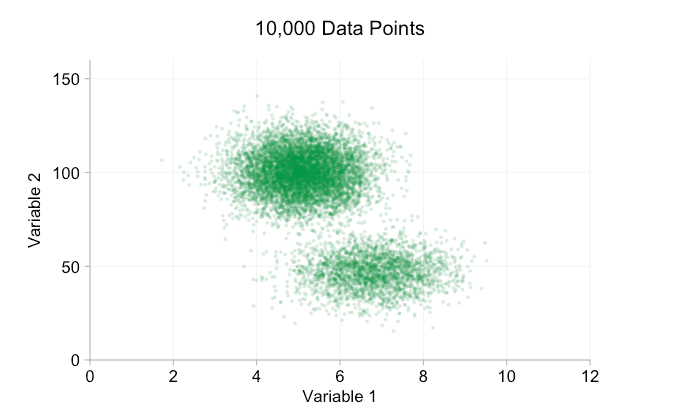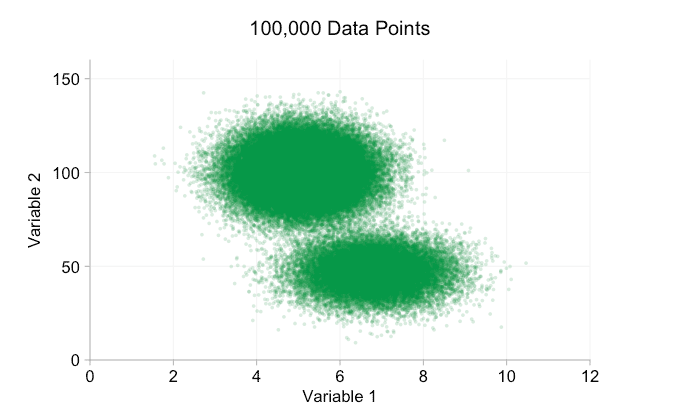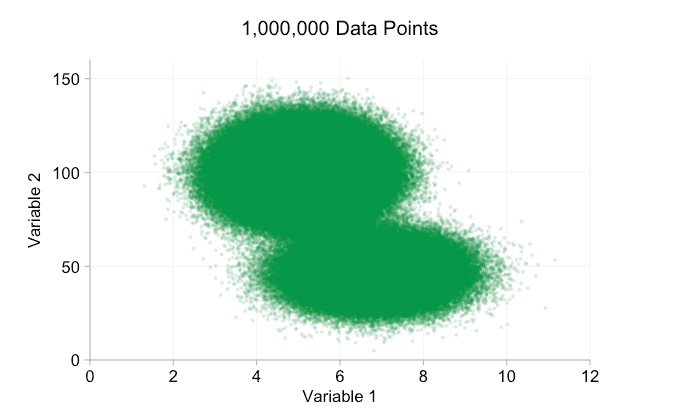
Estos refinamientos ciertamente ayudan cuando tenemos diez mil puntos de datos. Sin embargo, para cuando hemos alcanzado el millón de puntos, las dos distribuciones parecen haberse fusionado en una sola de nuevo. Hacer que los puntos sean más pequeños y transparentes podría ayudar a las cosas; Sin embargo, es posible que en algún momento tengamos que plantearnos un cambio de visualización. De eso hablaremos más adelante. Pero primero intentemos complementar nuestra visualización con información extra. Específicamente, visualicemos las distribuciones marginales. Tenemos varias opciones. Hay demasiados datos para un diagrama de alfombra, pero podemos agrupar los datos y mostrar histogramas. O podemos usar una opción más suave: un gráfico de densidad de kernel. Por último, podríamos utilizar la distribución acumulativa empírica. Esta última opción evita cualquier agrupación o suavizado, pero los resultados son probablemente menos intuitivos. Elegiré la opción de densidad del kernel aquí, pero es posible que prefiera un histograma. El gif animado de abajo es el mismo que el de arriba, pero con las distribuciones marginales suavizadas agregadas. He dejado las escalas apagadas para evitar el desorden y porque solo nos interesan realmente los juicios aproximados de la altura relativa.

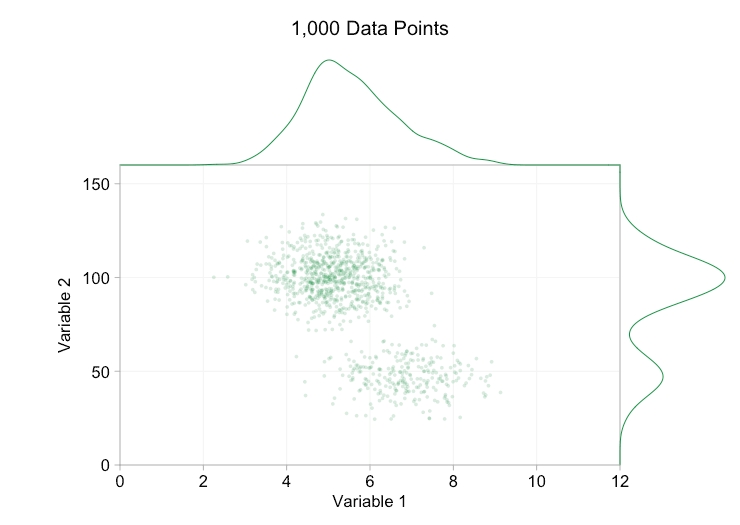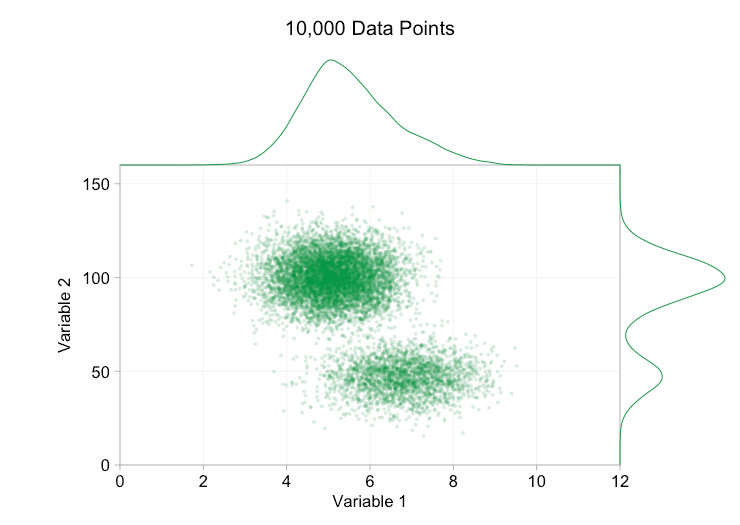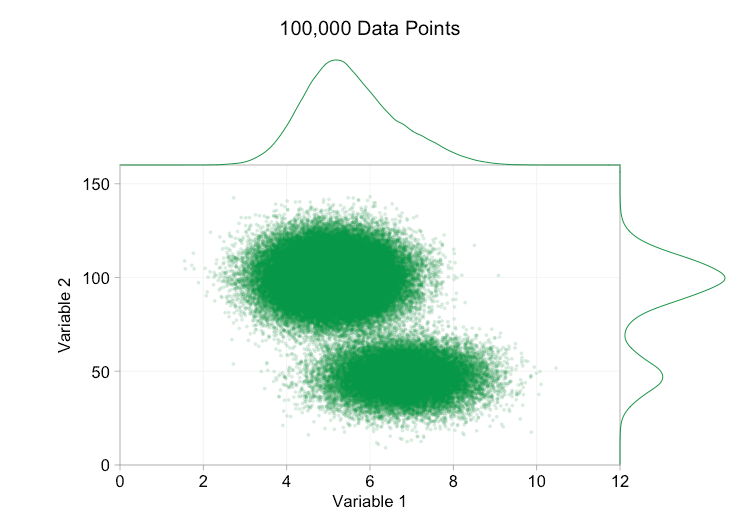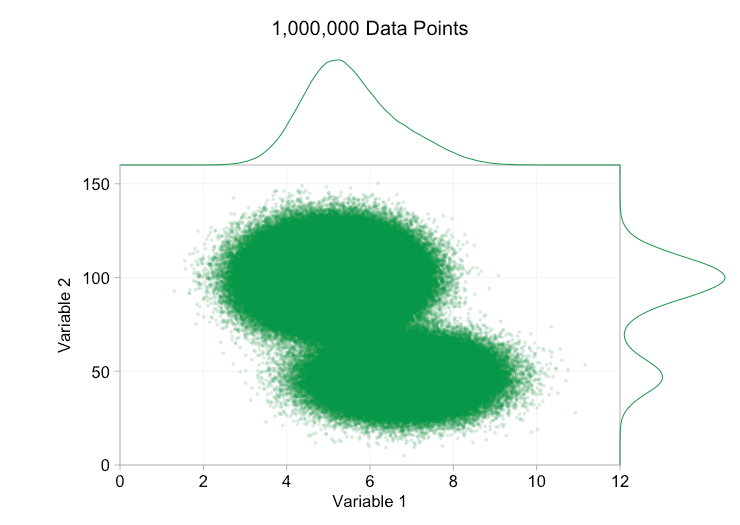
La adición de distribuciones marginales, en particular la distribución de la variable 2, ayuda a aclarar que hay dos distribuciones diferentes en los datos bivariados. La naturaleza de doble pico de la Variable 2 es evidente tanto si hay mil puntos de datos como si hay un millón. Los tamaños relativos de los dos componentes también son claros. Por el contrario, la distribución marginal de la variable 1 solo tiene un único pico, a pesar de provenir de dos distribuciones distintas. Esto debería dejar claro que la adición de distribuciones marginales no es de ninguna manera una solución universal a la sobregráfica en los diagramas de dispersión. Para reforzar este punto, la siguiente animación muestra un conjunto completamente diferente de puntos de datos (generados) en un diagrama de dispersión con distribuciones marginales. De nuevo, los datos proceden de una muestra aleatoria de dos distribuciones 2D diferentes, pero ambas distribuciones marginales del conjunto de datos completo no logran resaltar esta separación. Al igual que antes, cuando el número de puntos de datos es grande, la distinción entre los dos clústeres tampoco se puede ver en el diagrama de dispersión.

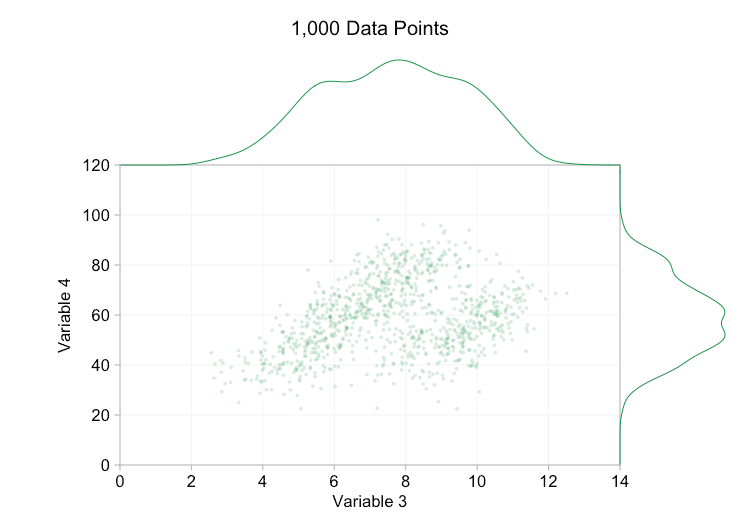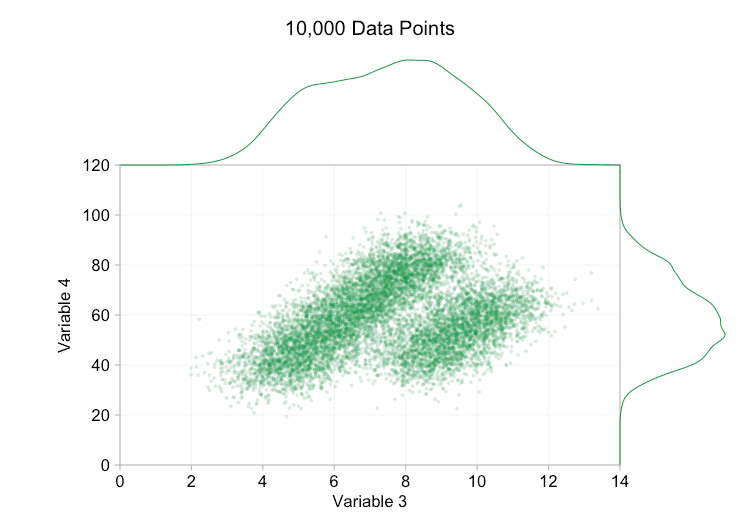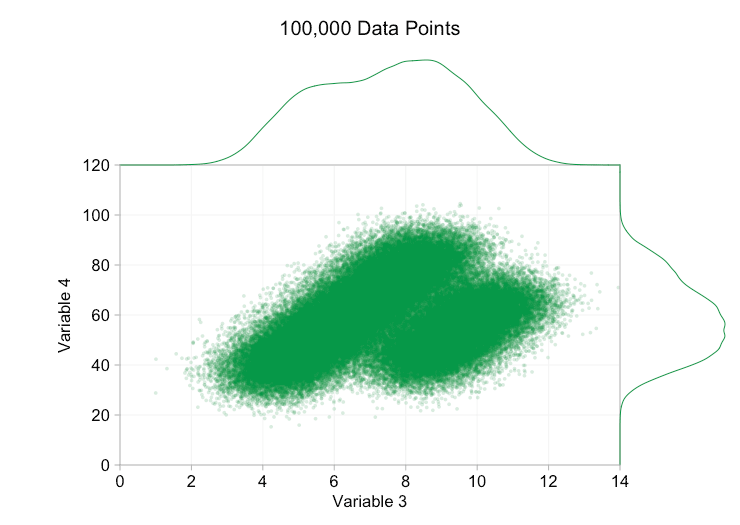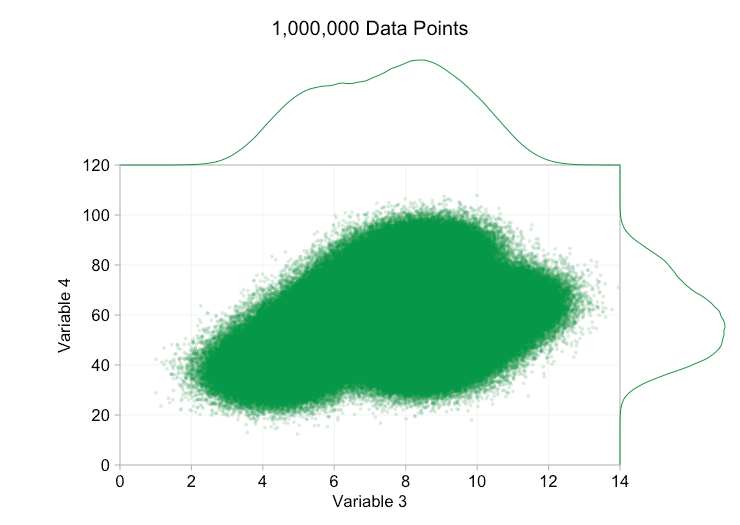
Volviendo al tamaño de los puntos y la opacidad, ¿qué obtenemos si hacemos que los puntos de datos sean muy pequeños y casi completamente transparentes?

Ahora podemos distinguir claramente dos clústeres en cada conjunto de datos. Sin embargo, es difícil distinguir cualquier detalle fino.

Dado que de todos modos hemos perdido ese detalle fino, parece adecuado preguntarse si realmente queremos dibujar un millón de puntos de datos. Puede ser tediosamente lento e imposible en ciertos contextos. Los histogramas 2D son una alternativa. Al agrupar los datos, podemos reducir el número de puntos a trazar y, si elegimos una escala de colores adecuada, seleccionar algunas de las características que se perdieron en el desorden del diagrama de dispersión. Después de experimentar un poco, elegí una escala de colores que iba desde el negro, pasando por el verde, hasta el blanco en el extremo superior. Tenga en cuenta que esto es (casi) lo contrario del efecto creado por el sobretrazado en los diagramas de dispersión anteriores.

En ambos histogramas 2D podemos ver claramente los dos grupos diferentes que representan las dos distribuciones de las que se extraen los datos. En el primer caso también podemos ver que hay más recuentos en el clúster superior izquierdo que en el grupo inferior derecho, un detalle que se pierde en el diagrama de dispersión con un millón de puntos de datos (pero más obvio a partir de las distribuciones marginales). Por el contrario, en el caso del segundo conjunto de datos podemos ver que las "alturas" de los dos clústeres son más o menos comparables.

Los gráficos 3D se usan en exceso, pero aquí (ver más abajo) creo que en realidad funcionan bastante bien en términos de proporcionar una imagen amplia de dónde están concentrados y dónde no se concentran los datos. La oclusión de características es un problema con los gráficos 3D, por lo que si va a seguir esta ruta al explorar sus propios datos, le recomiendo encarecidamente que utilice un software que permita la interacción del usuario a través de la rotación y el zoom.

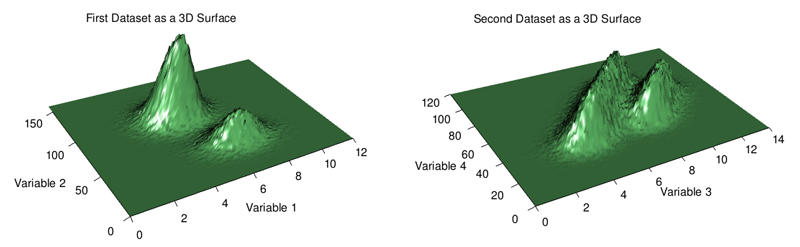
En resumen, los diagramas de dispersión son una forma sencilla y, a menudo, eficaz de visualizar datos bivariados. Sin embargo, si el gráfico sufre de un trazado excesivo, intente reducir el tamaño de los puntos y la opacidad. En su defecto, puede ser útil un histograma 2D o incluso un gráfico de superficie en 3D. En este último caso, tenga cuidado con la oclusión.