Introducción a los múltiplos pequeños

Los múltiplos pequeños (colecciones de gráficos pequeños (obviamente) en los que se trazan las mismas variables en cada gráfico, pero los datos de cada gráfico están condicionados en función de otra variable (o dos), se pueden utilizar para fines similares, con algunas ventajas y algunas desventajas.

En mi último artículo argumenté que todavía hay un lugar para los GIF en la visualización de datos en la web. Un GIF se puede utilizar para ilustrar cómo una medida o medidas han cambiado con el tiempo o varían en función de una tercera variable, categórica.

Aquí está el GIF de los cambios en la población a lo largo del tiempo de mi artículo anterior (los datos provienen del Banco Mundial):

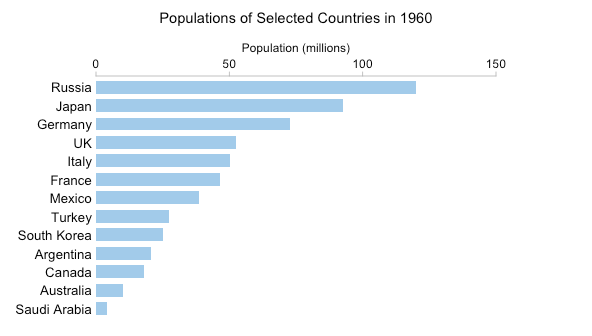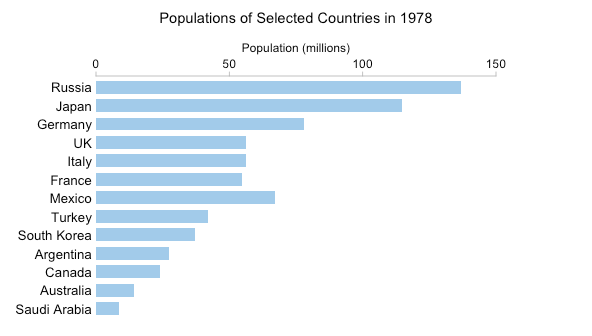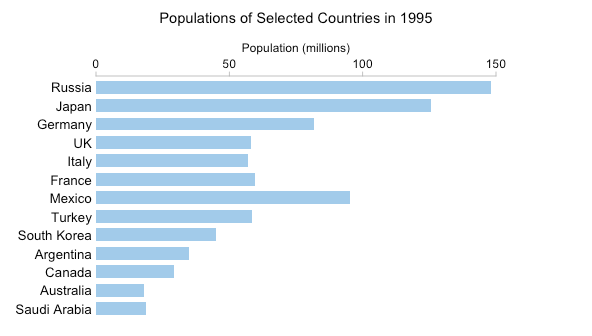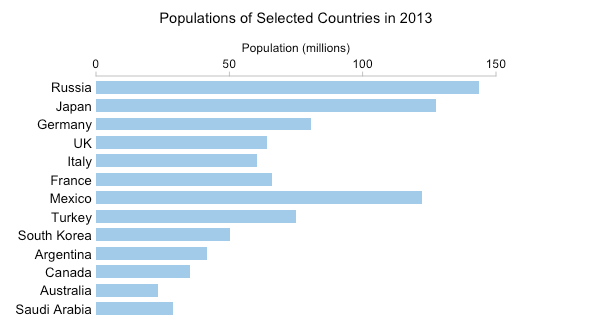
Ese GIF tiene 54 fotogramas separados. No es particularmente práctico crear un pequeño gráfico múltiple con 54 gráficos separados, pero aún así podemos tener una buena idea de los cambios que se están produciendo "muestreando" los datos cada seis años:

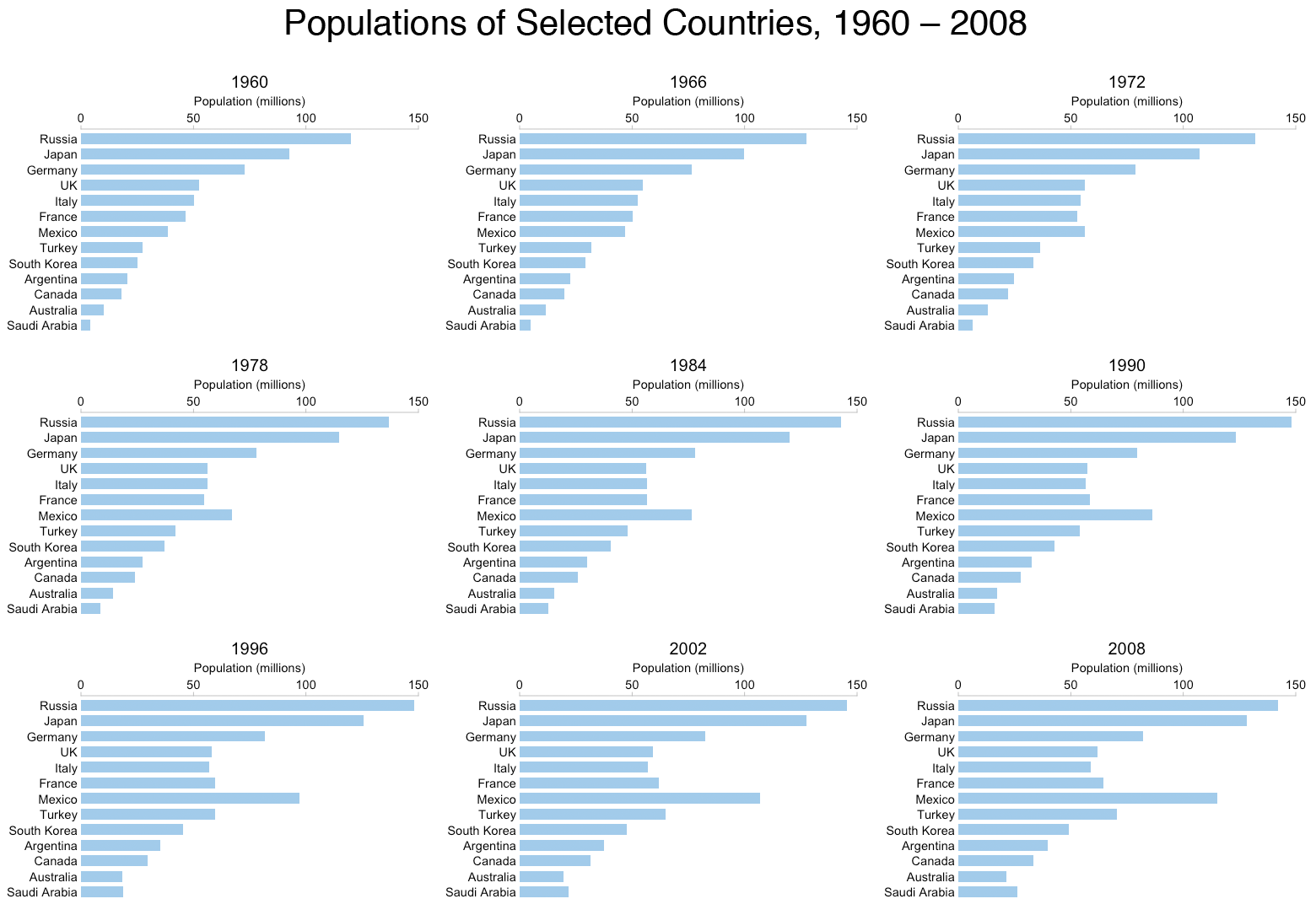
Obviamente, puede navegar por el pequeño diseño múltiple a su gusto. Se puede ver claramente el rápido aumento de la población de México, por ejemplo. Se puede ver que la población se duplicó de poco más de 50 millones en 1972 a poco más de 100 millones en 2002. Para obtener este tipo de información del GIF, debe mantener los detalles en la memoria de trabajo mientras espera que avancen los fotogramas.

Sin embargo, creo que el GIF hace que los cambios más sutiles sean más obvios. Los "bamboleos" (pequeños aumentos y disminuciones) en la población alemana que son fáciles de ver en el GIF están ausentes en el pequeño gráfico múltiple. Esto no se debe solo a la menor resolución temporal. Incluso si hubiera un gráfico para cada año, el pequeño tamaño de cada gráfico y la distancia entre ellos significaría que las pequeñas y sutiles oscilaciones probablemente pasarían desapercibidas.

En el artículo sobre GIFs también hice referencia a un gráfico anterior que creé usando los mismos datos, una variante en el slopegraph:

Deconstruir esta vista de los datos en gráficos de líneas separados y luego crear un marco GIF para cada país no fue particularmente útil. Pero, ¿qué pasa si en su lugar creamos un pequeño gráfico múltiple? He hecho esto a continuación, omitiendo Australia (bastante arbitrariamente) para facilitar el uso de una cuadrícula de 3 por 4.

Esto es más útil que la versión GIF. Por ejemplo, es mucho más fácil comparar países que no son espacialmente adyacentes en este gráfico que comparar países cuyos marcos no eran temporalmente adyacentes en el GIF. Pero ambos parecen inferiores a la variante del diagrama de pendiente que nos permite ver cruces de líneas (que indican cambios en el rango de la población) y más detalles en las oscilaciones de la población (como la de Alemania) debido a la mayor extensión vertical. Sin embargo, es posible que los datos de otros países no coincidan tan bien con el diseño básico del gráfico de pendientes. Como mencioné anteriormente, los gráficos de pendiente con frecuencia sufren problemas relacionados con etiquetas superpuestas. Esto no es un problema con la configuración múltiple pequeña.

Otra razón por la que la variante de gráfico de pendiente funciona bien en el ejemplo anterior es porque solo tenemos una línea por país, que muestra la población. Si tenemos más de una línea por país (u otra variable categórica) entonces este diseño ya no tiene sentido. Pero un diseño múltiple pequeño puede sobresalir en tal situación.

El siguiente gráfico muestra las estimaciones de la tasa bruta de natalidad y la tasa bruta de mortalidad (de nuevo del Banco Mundial) para una selección (bastante arbitraria) de nueve naciones del G-20.

A partir de esta figura podemos ver toda una serie de historias de datos interesantes (y, desafortunadamente, frecuentemente sombrías y deprimentes) sobre países individuales, tales como:

• El aumento de la tasa de natalidad y la caída de la tasa de mortalidad en la China de la década de 1960 tras el final del período del Gran Salto Adelante;
• El aumento, a partir de mediados del decenio de 1990, de la tasa de mortalidad en Sudáfrica debido a la epidemia de SIDA y la disminución en los últimos años a medida que los medicamentos antirretrovirales se ampliaron considerables;
• The hinoeuma year (1966) in Japan.

Al mismo tiempo, la figura nos permite contrastar y comparar. Por ejemplo, un patrón de bajas tasas de mortalidad y tasas de natalidad aún más bajas conduce a una población envejecida (al menos en ausencia de una migración significativa). En consecuencia, una lectura rápida de la cifra y probablemente no se sorprendería al saber que en los últimos años se han visto preocupaciones sobre las pensiones y la edad de jubilación en Italia, Alemania y Japón.

Hasta ahora, los ejemplos no han establecido ninguna distinción entre los componentes horizontales y verticales de una pequeña "cuadrícula" múltiple. Pero, al igual que con los gráficos de líneas y los diagramas de dispersión, podemos codificar diferentes variables en nuestras dos dimensiones diferentes. El siguiente gráfico del Estudio de Visualización Científica de la NASA (vale la pena descargar el archivo TIFF de alta resolución por ti mismo) que muestra la variación en la extensión del hielo en el Polo Norte codifica el año en la dirección horizontal (de 1979 a 2014) y el mes en la dirección vertical. Cada columna muestra cómo cambió la extensión del hielo a lo largo del año, mientras que cada fila muestra los cambios a largo plazo para un mes en particular.

Una vez más, es importante recalcar que la elección del gráfico depende de dónde se vaya a colocar y de quién lo vaya a ver. A pesar de que cada gráfico individual es pequeño, una pequeña cuadrícula múltiple puede ocupar un espacio considerable. Con navegadores pequeños en los teléfonos, esto puede ser un obstáculo importante.